Maximization of banana function by various methods
Contents
Maximization of banana function by various methods¶
Randall Romero Aguilar, PhD
This demo is based on the original Matlab demo accompanying the Computational Economics and Finance 2001 textbook by Mario Miranda and Paul Fackler.
Original (Matlab) CompEcon file: demopt04.m
Running this file requires the Python version of CompEcon. This can be installed with pip by running
!pip install compecon --upgrade
Last updated: 2022-Oct-23
\[f(x,y)=-100*(y-x^2)^2-(1-x)^2\]
starting at [0,1].
import numpy as np
from compecon import OP
np.set_printoptions(4, linewidth=120, suppress=True)
import matplotlib.pyplot as plt
''' Set up the problem '''
x0 = [1, 0]
banana = OP(lambda x: -100 * (x[1] - x[0] ** 2)**2 - (1 - x[0]) ** 2,
x0, maxit=250, print=True, all_x=True)
x = banana.qnewton()
J = banana.jacobian(x)
E = np.linalg.eig(banana.hessian(x))[0]
print('x = ', x, '\nJ = ', J, '\nE = ', E)
0 0 6.56e-01
1 0 1.22e-01
2 0 1.43e-02
3 0 4.66e-03
4 0 1.18e-01
5 0 2.03e-02
6 0 4.83e-02
7 0 2.29e-01
8 0 5.16e-02
9 0 7.99e-02
10 0 6.84e-02
11 0 1.82e-01
12 0 4.10e-02
13 0 6.38e-02
14 0 2.03e-01
15 0 7.79e-02
16 0 5.22e-02
17 0 1.48e-01
18 0 6.66e-02
19 0 2.97e-02
20 0 6.03e-02
21 0 1.81e-03
22 0 9.11e-03
23 0 1.73e-03
24 0 9.07e-05
25 0 7.26e-07
26 0 1.01e-09
x = [1. 1.]
J = [-0. 0.]
E = [-1001.6006 -0.3994]
''' Plots options '''
steps_options = {'marker': 'o',
'color': (0.2, 0.2, .81),
'linewidth': 1.0,
'markersize': 3,
'markerfacecolor': 'white',
'markeredgecolor': 'red'}
contour_options = {'levels': -np.exp(np.arange(7,0.25,-0.5)),
'colors': '0.25',
'linewidths': 0.5}
''' Data for coutours '''
n = 40 # number of grid points for plot per dimension
xmin = [-0.7, -0.2]
xmax = [ 1.2, 1.2]
X0, X1 = np.meshgrid(*[np.linspace(a, b, n) for a, b in zip(xmin, xmax)])
Y = banana.f([X0.flatten(), X1.flatten()])
Y.shape = (n, n)
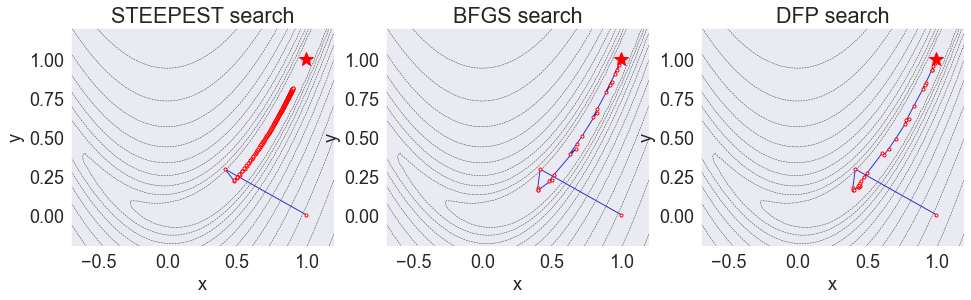
fig, axs = plt.subplots(1, 3, figsize=[16,4])
for ax, method in zip(axs, banana.search_methods.keys()):
''' Solve problem with given method '''
print('\n\nMaximization with method ' + method.upper())
x = banana.qnewton(SearchMeth=method)
print('x =', x)
''' Plot the result '''
ax.set(title=method.upper() + " search",
xlabel='x',
ylabel='y',
xlim=[xmin[0], xmax[0]],
ylim=[xmin[1], xmax[1]])
ax.contour(X0, X1, Y, **contour_options)
ax.plot(*banana.x_sequence, **steps_options)
ax.plot(1, 1, 'r*', markersize=15)
Maximization with method STEEPEST
0 0 6.56e-01
1 0 1.01e-01
2 0 8.28e-03
3 0 2.87e-02
4 0 7.67e-03
5 0 2.73e-02
6 0 7.05e-03
7 0 2.56e-02
8 0 6.49e-03
9 0 2.38e-02
10 0 5.98e-03
11 0 2.22e-02
12 0 5.54e-03
13 0 2.07e-02
14 0 5.14e-03
15 0 1.94e-02
16 0 4.80e-03
17 0 1.81e-02
18 0 4.49e-03
19 0 1.70e-02
20 0 4.22e-03
21 0 1.60e-02
22 0 3.98e-03
23 0 1.51e-02
24 0 3.76e-03
25 0 1.43e-02
26 0 3.57e-03
27 0 1.36e-02
28 0 3.39e-03
29 0 1.29e-02
30 0 3.23e-03
31 0 1.23e-02
32 0 3.08e-03
33 0 1.17e-02
34 0 2.95e-03
35 0 1.12e-02
36 0 2.82e-03
37 0 1.07e-02
38 0 2.71e-03
39 0 1.03e-02
40 0 2.60e-03
41 0 9.86e-03
42 0 2.50e-03
43 0 9.48e-03
44 0 2.41e-03
45 0 9.12e-03
46 0 2.33e-03
47 0 8.78e-03
48 0 2.25e-03
49 0 8.47e-03
50 0 2.17e-03
51 0 8.18e-03
52 0 2.10e-03
53 0 7.90e-03
54 0 2.04e-03
55 0 7.64e-03
56 0 1.98e-03
57 0 7.40e-03
58 0 1.92e-03
59 0 7.17e-03
60 0 1.86e-03
61 0 6.95e-03
62 0 1.81e-03
63 0 6.74e-03
64 0 1.76e-03
65 0 6.55e-03
66 0 1.71e-03
67 0 6.36e-03
68 0 1.67e-03
69 0 6.18e-03
70 0 1.62e-03
71 0 6.02e-03
72 0 1.58e-03
73 0 5.86e-03
74 0 1.54e-03
75 0 5.70e-03
76 0 1.51e-03
77 0 5.56e-03
78 0 1.47e-03
79 0 5.42e-03
80 0 1.44e-03
81 0 5.28e-03
82 0 1.40e-03
83 0 5.16e-03
84 0 1.37e-03
85 0 5.03e-03
86 0 1.34e-03
87 0 4.92e-03
88 0 1.31e-03
89 0 4.80e-03
90 0 1.29e-03
91 0 4.70e-03
92 0 1.26e-03
93 0 4.59e-03
94 0 1.23e-03
95 0 4.49e-03
96 0 1.21e-03
97 0 4.39e-03
98 0 1.18e-03
99 0 4.30e-03
100 0 1.16e-03
101 0 4.21e-03
102 0 1.14e-03
103 0 4.13e-03
104 0 1.12e-03
105 0 4.04e-03
106 0 1.10e-03
107 0 3.96e-03
108 0 1.08e-03
109 0 3.88e-03
110 0 1.06e-03
111 0 3.81e-03
112 0 1.04e-03
113 0 3.74e-03
114 0 1.02e-03
115 0 3.67e-03
116 0 1.00e-03
117 0 3.60e-03
118 0 9.86e-04
119 0 3.53e-03
120 0 9.69e-04
121 0 3.47e-03
122 0 9.53e-04
123 0 3.41e-03
124 0 9.37e-04
125 0 3.35e-03
126 0 9.22e-04
127 0 3.29e-03
128 0 9.07e-04
129 0 3.23e-03
130 0 8.93e-04
131 0 3.17e-03
132 0 8.79e-04
133 0 3.12e-03
134 0 8.65e-04
135 0 3.07e-03
136 0 8.52e-04
137 0 3.02e-03
138 0 8.39e-04
139 0 2.97e-03
140 0 8.26e-04
141 0 2.92e-03
142 0 8.14e-04
143 0 2.88e-03
144 0 8.02e-04
145 0 2.83e-03
146 0 7.90e-04
147 0 2.79e-03
148 0 7.79e-04
149 0 2.74e-03
150 0 7.68e-04
151 0 2.70e-03
152 0 7.57e-04
153 0 2.66e-03
154 0 7.46e-04
155 0 2.62e-03
156 0 7.36e-04
157 0 2.58e-03
158 0 7.26e-04
159 0 2.54e-03
160 0 7.16e-04
161 0 2.51e-03
162 0 7.06e-04
163 0 2.47e-03
164 0 6.97e-04
165 0 2.43e-03
166 0 6.88e-04
167 0 2.40e-03
168 0 6.79e-04
169 0 2.37e-03
170 0 6.70e-04
171 0 2.33e-03
172 0 6.61e-04
173 0 2.30e-03
174 0 6.53e-04
175 0 2.27e-03
176 0 6.45e-04
177 0 2.24e-03
178 0 6.36e-04
179 0 2.21e-03
180 0 6.29e-04
181 0 2.18e-03
182 0 6.21e-04
183 0 2.15e-03
184 0 6.13e-04
185 0 2.12e-03
186 0 6.06e-04
187 0 2.09e-03
188 0 5.98e-04
189 0 2.07e-03
190 0 5.91e-04
191 0 2.04e-03
192 0 5.84e-04
193 0 2.01e-03
194 0 5.77e-04
195 0 1.99e-03
196 0 5.71e-04
197 0 1.96e-03
198 0 5.64e-04
199 0 1.94e-03
200 0 5.57e-04
201 0 1.92e-03
202 0 5.51e-04
203 0 1.89e-03
204 0 5.45e-04
205 0 1.87e-03
206 0 5.39e-04
207 0 1.85e-03
208 0 5.33e-04
209 0 1.82e-03
210 0 5.27e-04
211 0 1.80e-03
212 0 5.21e-04
213 0 1.78e-03
214 0 5.15e-04
215 0 1.76e-03
216 0 5.10e-04
217 0 1.74e-03
218 0 5.04e-04
219 0 1.72e-03
220 0 4.99e-04
221 0 1.70e-03
222 0 4.93e-04
223 0 1.68e-03
224 0 4.88e-04
225 0 1.66e-03
226 0 4.83e-04
227 0 1.64e-03
228 0 4.78e-04
229 0 1.62e-03
230 0 4.73e-04
231 0 1.61e-03
232 0 4.68e-04
233 0 1.59e-03
234 0 4.63e-04
235 0 1.57e-03
236 0 4.58e-04
237 0 1.55e-03
238 0 4.54e-04
239 0 1.54e-03
240 0 4.49e-04
241 0 1.52e-03
242 0 4.44e-04
243 0 1.50e-03
244 0 4.40e-04
245 0 1.49e-03
246 0 4.36e-04
247 0 1.47e-03
248 0 4.31e-04
249 0 1.46e-03
x = None
Maximization with method BFGS
0 0 6.56e-01
1 0 1.22e-01
2 0 1.43e-02
3 0 4.66e-03
4 0 1.18e-01
5 0 2.03e-02
6 0 4.83e-02
7 0 2.29e-01
8 0 5.16e-02
9 0 7.99e-02
10 0 6.84e-02
11 0 1.82e-01
12 0 4.10e-02
13 0 6.38e-02
14 0 2.03e-01
15 0 7.79e-02
16 0 5.22e-02
17 0 1.48e-01
18 0 6.66e-02
19 0 2.97e-02
20 0 6.03e-02
21 0 1.81e-03
22 0 9.11e-03
23 0 1.73e-03
24 0 9.07e-05
25 0 7.26e-07
26 0 1.01e-09
x = [1. 1.]
Maximization with method DFP
0 0 6.56e-01
1 0 1.22e-01
2 0 1.44e-02
3 0 4.18e-03
4 0 5.11e-02
5 0 1.01e-02
6 0 1.37e-03
7 0 6.86e-03
8 0 4.13e-03
9 0 2.07e-02
10 0 9.68e-03
11 0 3.70e-02
12 0 3.44e-02
13 0 1.68e-01
14 0 1.81e-02
15 0 5.11e-02
16 0 8.17e-02
17 0 1.57e-01
18 0 4.33e-02
19 0 2.72e-02
20 0 1.07e-01
21 0 1.70e-01
22 0 4.06e-02
23 0 2.57e-02
24 0 1.13e-01
25 0 1.33e-03
26 0 2.36e-02
27 0 2.46e-02
28 0 2.46e-02
29 0 3.34e-04
30 0 4.21e-04
31 0 4.57e-06
32 0 1.54e-07
33 0 1.52e-11
x = [1. 1.]
Using Scipy¶
As of this version of CompEcon, the Nelder Mead method has not been implemented. However, we can still use it with the help of the scipy.optimize.minimize function. To this end, we must rewrite the banana function (change its sign) so that we switch from our original maximization problem to one of minimization.
from scipy.optimize import minimize
x0 = [1, 0]
def banana2(x):
return 100 * (x[1] - x[0] ** 2)**2 + (1 - x[0]) ** 2
res = minimize(banana2, x0, method='Nelder-Mead')
print(res)
final_simplex: (array([[1. , 1.0001],
[1. , 1. ],
[1. , 1. ]]), array([0., 0., 0.]))
fun: 1.0078716929461423e-09
message: 'Optimization terminated successfully.'
nfev: 148
nit: 79
status: 0
success: True
x: array([1. , 1.0001])
